今回の数学は、円周角の定理とモンテーホール問題について学びました。
先生は筑波大の大学院生の方で、みんなよりちょっとだけ年上のお兄さん。数学の教員免許もちゃんと持っていて、他の高校でもお仕事をされています。

円周角の定理は
1つの弧に対する円周角の大きさは一定であり、その弧に対する中心角の半分である。
というもので、
円周角が等しいとき、その弧の長さも等しい
弧の長さが等しいとき、それに対する円周角も等しい
というと、、なに?
という感じなので、こんな実験をしました。

- 生徒Aと生徒Bが適当な距離を取って立つ。
- 生徒C(カメラ担当)が、生徒Aと生徒Bがスマホの画面の両端に映る位置に立つ。
- 生徒Cは、生徒Aと生徒Bが画面の両端に映り続けるようにしながら、ゆっくりと移動する。
- 生徒Cは移動しながら写真を撮る。
- 生徒Cの移動経路を他の生徒が記録するする。
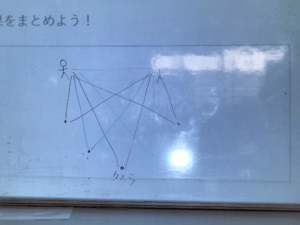
という手順でワイワイ楽しみながら、円周角の定理を実体験することできました。
続いて、モンティ・ホール問題という数学の問題に取り組みました。
確率の問題です。
モンティ・ホール問題の元になったゲームは、アメリカのテレビ番組『レッツ・メイク・ア・ディール(Let’s Make a Deal)』で行われていた一連のゲームの一部で、この番組では、参加者が複数の選択肢から賞品を選ぶ機会が与えられ、司会者のモンティ・ホールさんという方がその進行を務めていました。そのモンティ・ホールさんの名前を取ってモンティ・ホール問題と呼ばれています。

モンティ・ホール問題は3つの扉が用意され、1つのは後ろにアタリの高級車、あと二つはハズレのヤギがいて、アタリがば回答者は高級車がもらえるというものでした。
しかし、モンティ・ホールさんは回答者が扉を選んでから、ハズレの扉を1つ開き回答者の心を揺さぶるというスタイルを取っていました。
これを実際に30回やって、モンティホールさんの揺さぶりによってどうなるかを検証してみると意外な結果になりました。高級車もなければヤギがいるわけでもないんですけどね。
道具は扉は紙コップ、アタリとして消しゴム、ハズレは空っぽです。
30回やった結果はどの生徒もアタリが20回前後正解が出ていました。変えるのが面倒で、全然変えなかった少数派はアタリは10回前後になっていました。
先生の説明によるとこんなことが起きていました。
- 3つのうちの1つの扉を選だ時、ハズレを選んでいる確率が高いのでハズレを選んでいると仮定(ハズレの確率2/3)
- モンティホールさんに1つハズレの扉が開かれた
- 仮定としては自分はハズレを開いている
- 扉が二つになっている。もう一つの扉はアタリ可能性が高い
- 変えたらそれはあたりになる可能性が高い(アタリの確率2/3)
んじゃ、さいごはとりあえず変えたほうがいい!
最初にアタリを選んでいて変えたらハズレますが、最初にハズレを選んで変えれば絶対にアタリなんですよね。
つまりはモンティ・ホールさんの揺さぶりに素直に揺さぶられて、ドアを変えれば3つのドアうち2はアタリと同じなんです。最初にアタリ引いてたら外れちゃいますけどね(笑)
確率ってすごいですね。
興味深く楽しいあっというまの2時間でした😊



